実際に調査するのが難しいような事を、いくつかの情報を元に論理的に短時間で計算し、推論することをフェルミ推定といいます。
就活経験者ならお馴染みですかね?
フェルミ推定をする際に必要となるのは
- 一般常識・データ
- 論理的な思考力
なので、就活に限らずその人の「頭の良さ」を推し量るのに用いられます。
要するに「一般常識のない人」「論理的思考力のない人」を洗い出したり、「面白い発想の人」「計算能力の高い人」を洗い出すのに使われている訳ですね。
フェルミ推定のポイントは
「見えている情報から見えない情報を推測する」
という点です。
いろいろな事に使えそうですね?
欧米なんかだと学校教育にも取り入れられているそうですよ。
例えばお散歩中にラーメン屋を通りかかったら
→人気度を考慮しながら概算で加重平均
→売上単価を計算
→見た日時から曜日・時間帯別に推定する
→売上数量を計算
→地域から時給を計算
→日時と人数から時間当たりの客の回転数を計算
→人件費・売上数量の計算
→地域・面積から相場を計算
→販管費の計算
などの目に見える情報から
などを推定してニヤニヤしたりします。
あまり利益が出ていなそうだったら潰れる前に食べに行ったりもします。
(このケースではある程度の会計・原価・不動産価格の知識が前提となる)
ラーメン屋の場合は正解を確認しづらいのですが、
「ここって月商○○○○万なんだってね。すごい儲かってるねぇ」
とか言えばその反応である程度の正解が分かります。
正解が確実にわかることで練習をし精度を上げていくことができます。
たとえば不動産広告の
「場所」
「築年数」
「平米数」
だけを見て、
「販売価格」
を推定すると不動産関係の相場感が身につきます。
または練習問題の載っている本などもあります。
フェルミ推定
で、そんなことはどうでも良くて、
ここではこの
「フェルミ推定を様々な事(特に投資判断)に活かそう」
という趣旨で書いていきます。
その前にフェルミ推定に使える幾つかの法則を紹介します。
もくじ(見出しのまとめ)
ハインリッヒの法則
これは「経済学の保険の論点」や統計学(経営学でも出てきたかな?)で出てくるのでご存じの方も多いと思います。
簡単に説明すると、
「1つの重大事故の背後には29の軽微な事故があり、その背景には300の異常が存在する」
というものです。
何やら使えそうですね?
ハインリッヒの法則と同様に、バードの法則、タイピアソン則などもあります。
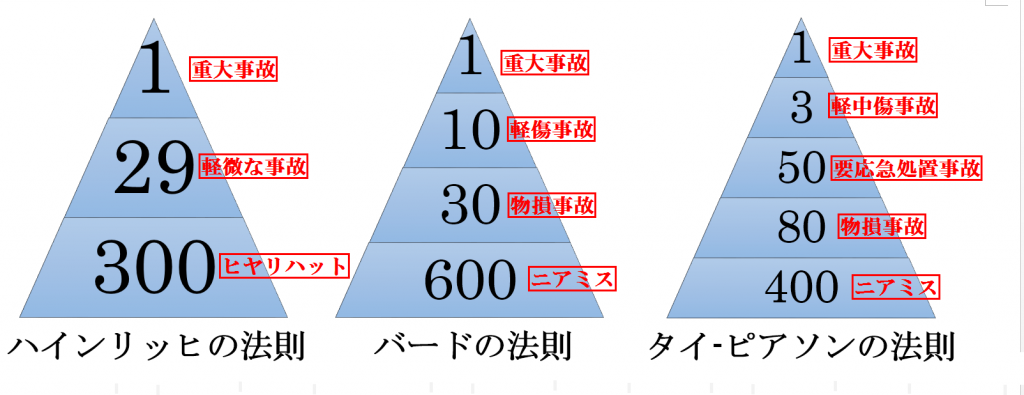
これらは統計的に事故の比率を表したものです。
まぁハインリッヒの法則だけ覚えておけばとりあえずは十分だと思います。
よくわからんという人は
「超ヤバイこと1」「ヤバイこと29」「未遂300」に置き換えてください。
(29が嫌であればなんなら30でもいいです)
「いい肉300!」と覚えてしまえば一発です。
で、このハインリッヒの法則はフェルミ推定を行う上でも結構役立ったりします。
例えば、
殺人(超ヤバイこと)が1件あったら、
その手前の傷害事件(ヤバイこと)は29件あるのでは?
と考えられます。
実際犯罪白書を見てみると、例年殺人は1000件程度に対し、傷害事件は30000件弱になっています。
ハインリッヒの法則をこれに当て嵌めることが妥当だとするなら、このデータに不自然な点はありません。
一方で性犯罪に関しては
強姦(超ヤバイこと)が例年1200件程度なのに対し、その他の性犯罪(ヤバイこと)を合わせると10000件程度にしかなりません。
ここで
「なんだこの法則使えないな」
とは私は考えません。
「何かしらがデータを歪めているのではないか」
「法則への当てはめ方が間違っているのではないか」
と考えます。
性犯罪の場合、発生したとしても被害者が泣き寝入りするというのはよく聞きますね。
これがデータを歪めてしまっているのでしょう。
各都道府県で一日に20件くらいのペースです。
(もっと多そう・・・ということは強姦でも認知できていない件数が多そうですね)
ハインリッヒの法則を使う場合には、データが正確であることが前提です。
逆に言えばこの比率が当てはまらない場合には、「データがおかしい」「当てはめがおかしい」と考えましょう。
特に、使う場合にはデータの背景に注意しましょう。
また、何をどこに当て嵌めるかでも結果が変わってしまいます。
とはいえ、そんな面倒くさい使い方をせずとも
目の前で「(超)ヤバイこと」が発生したときに、
「これは他にもたくさん起こっているかもしれない」
と考えることができるのがハインリッヒの法則の良い点です。
自身の警戒心を強めることができます。
これはハインリッヒの法則に当てはめるとどの部分に当てはまるでしょうか?
また、当てはめた場合同様に杭のないマンションはその比率で既に見つかっていますか?
問題が顕在化していないマンションは全国で何件くらい隠れていると思いますか?
こわいですねぇ
投資にも応用できる?
ハインリッヒの法則を使えば論理的な思考を放棄していたとしてもある程度フェルミ推定ができますね。
投資においてはどうでしょうか?
インサイダー取引や見せ玉などで逮捕される人が時々いますね。
実際にマーケットでこういった不正をしているのは逮捕された人だけな訳がありません。
いろいろな前提条件に立って計算してみると良いでしょう。
その上で性悪説に基づいた戦略を練りましょう。
裁量トレードの際に、何かしらのイレギュラーな事象が起こったら特に要注意です。
板や出来高、各種テクニカルなどに何かしらの異変を見つけたのであれば、すぐに警戒心を強め何が起きているのか見定めなければなりません。
目に見えるほどの異変があるのであれば、もうそれは相当ヤバイ時ですよ。
ハインリッヒの法則を知っていれば一瞬で必要な情報の概算が出せる時もあります。
その他、企業の財務情報や不正などに関してもハインリッヒの法則はある程度使えます。
これについては具体的なことは書きません。
自分で試行錯誤してみてください。
大切なのは、
「どこに当て嵌めるか」
です。
また
「当て嵌まらない場合何が原因か」
を考えると面白いことがわかる時もあります。
まとめ
フェルミ推定は脳トレ代わりに普段から行うとどんどん精度が上がっていきます。
クイズ形式で楽しみながらやるとよいでしょう。
また、中にはハインリッヒの法則を神格化し黄金則のように扱う人もいますが、ハインリッヒの法則は絶対的なものでは決してありません。
統計的に正しくてもそれは計量的なものであって、定性的な要因を無視してしまう場合もあり得ます。
とはいえ楽しみながら色んなデータで遊んでみるのが良いと思います。
